Tabla z

MODA, MEDIANA Y MEDIA 

La media, la mediana y la moda son herramientas estadísticas básicas y fáciles de calcular.

1.LA MEDIA. La media, también conocida como promedio, es el valor que se obtiene al dividir la suma de un conglomerado de números entre la cantidad de ellos.

Algunas características de la media son:

• Considera todas las puntuaciones
• El numerador de la fórmula es la cantidad de valores
• Cuando hay puntuaciones extremas, no tiene una representación exacta de la muestra.

Ejemplo:

En una tienda mayorista se quiere calcular el promedio de ventas que realizaron los empleados durante el mes. Para calcular la media se realiza lo siguiente:

1.1 LA MEDIA PARA DATOS AGRUPADOS:

 FÓRMULA:

 

  fi: frecuencia

  Xi: punto medio de clase

  n: total de frecuencias 

EJEMPLO:

2. MEDIANA: La mediana es un conjunto es un valor que se encuentra a la mitad de los otros valores, es decir, que al ordenar los número de menor a mayor, éste se encuentra justamente en medio entre los que están por arriba.

Algunas características de la media son:

• Las operaciones para calcular el valor son muy sencillas de realizar.
• La medida no depende de los valores de las variables, solamente de su orden.
• Generalmente, los valores son enteros.
• Se puede calcular aunque los números que se encuentren arriba y abajo no tengan límites.

EJEMPLO:

• La cantidad de valores es impar

Si se tienen los valores: 9,5,4,2,7, se ordenan: 2, 4, 5, 7, 9. El elemento de en medio es el 5, ya que se encuentra dos valores por encima y dos valores por debajo.

• La cantidad de valores es par

Si se tienen los valores 9,5,4,2, se ordenan: 2,4,5,9. En este caso se toman los dos valores centrales 5 y 4, la mediana es el promedio de ambos: 4.5

2.1 MEDIANA PARA DATOS AGRUPADOS:

EJEMPLO:

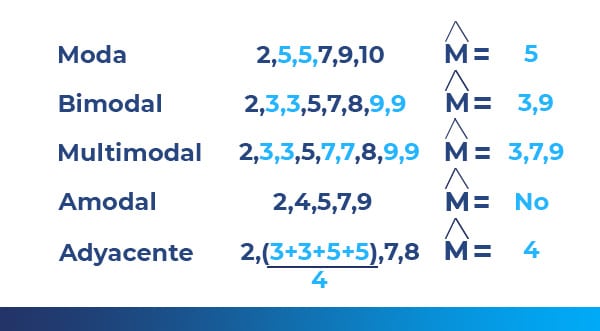
3. MODA. La moda es el valor que aparece más dentro de un conglomerado. En un grupo puede haber dos modas y se conoce como bimodal, y más de dos modas o multimodal cuando se repiten más de dos valores; se llama amodal cuando en un conglomerado no se repiten los valores.

Por último, se conoce como moda adyacente cuando dos valores continuos tienen la misma cantidad de repeticiones. En este caso se saca el promedio de ambos.

Las principales características de la moda son:

• Es una muestra muy clara
• Las operaciones para determinar el resultado son muy fáciles de elaborar
• Los valores que se presentan pueden ser cualitativos y cuantitativos.

EJEMPLO:

3.1 MODA PARA DATOS AGRUPADOS:

4. VENTAJAS Y DESVENTAJAS: